Scaling laws for dominant assurance contracts

~ Jessica Taylor

(note: this post is high in economics math, probably of narrow interest)

Dominant assurance contracts are a mechanism proposed by Alex Tabarrok for funding public goods. The following summarizes a 2012 class paper of mine on dominant assurance contracts. Mainly, I will be determining how much the amount of money a dominant assurance contract can raise as a function of how much value is created for how many parties, under uncertainty about how much different parties value the public good. Briefly, the conclusion is that, while Tabarrok asserts that the entrepreneur’s profit is proportional to the number of consumers under some assumptions, I find it is proportional to the square root of the number of consumers under these same assumptions.

The basic idea of assurance contracts is easy to explain. Suppose there are N people (“consumers”) who would each benefit by more than $S > 0 from a given public good (say, a piece of public domain music) being created, e.g. a park (note that we are assuming linear utility in money, which is approximately true on the margin, but can’t be true at limits). An entrepreneur who is considering creating the public good can then make an offer to these consumers. They say, everyone has the option of signing a contract; this contract states that, if each other consumer signs the contract, then every consumer pays $S, and the entrepreneur creates the public good, which presumably costs no more than $NS to build (so the entrepreneur does not take a loss).

Under these assumptions, there is a Nash equilibrium of the game, in which each consumer signs the contract. To show this is a Nash equilibrium, consider whether a single consumer would benefit by unilaterally deciding not to sign the contract in a case where everyone else signs it. They would save $S by not signing the contract. However, since they don’t sign the contract, the public good will not be created, and so they will lose over $S of value. Therefore, everyone signing is a Nash equilibrium. Everyone can rationally believe themselves to be pivotal: the good is created if and only if they sign the contract, creating a strong incentive to sign.

Tabarrok seeks to solve the problem that, while this is a Nash equilibrium, signing the contract is not a dominant strategy. A dominant strategy is one where one would benefit by choosing that strategy (signing or not signing) regardless of what strategy everyone else takes. Even if it would be best for everyone if everyone signed, signing won’t make a difference if at least one other person doesn’t sign. Tabarrok solves this by setting a failure payment $F > 0, and modifying the contract so that if the public good is not created, the entrepreneur pays every consumer who signed the contract $F. This requires the entrepreneur to take on risk, although that risk may be small if consumers have a sufficient incentive for signing the contract.

Here’s the argument that signing the contract is a dominant strategy for each consumer. Pick out a single consumer and suppose everyone else signs the contract. Then the remaining consumer benefits by signing, by the previous logic (the failure payment is irrelevant, since the public good is created whenever the remaining consumer signs the contract).

Now consider a case where not everyone else signs the contract. Then by signing the contract, the remaining consumer gains $F, since the public good is not created. If they don’t sign the contract, they get nothing and the public good is still not created. This is still better for them. Therefore, signing the contract is a dominant strategy.

What if there is uncertainty about how much the different consumers value the public good? This can be modeled as a Bayesian game, where agents (consumers and the entrepreneur) have uncertainty over each other’s utility function. The previous analysis assumed that there was a lower bound $T on everyone’s benefit from the public good. So, it still applies under some uncertainty, as long as there is a lower bound. For example, if each consumer’s utility in the good is uniformly distributed in [$1, $2], then S can be set to $0.999, and the argument still goes through, generating about $N of revenue to fund the public good.

However, things are more complicated when the lower bound is 0. Suppose each consumer’s benefit from the public good is uniformly distributed in [$0, $1] (Tabarrok writes “G” for the CDF of this distribution). Then, how can the entrepreneur set S so as to ensure that the good is created and they receive enough revenue to create it? There is no non-zero T value that is a lower bound, so none of the previous arguments apply.

Let’s modify the setup somewhat so as to analyze this situation. In addition to setting S and F, the entrepreneur will set K, the threshold number of people who have to sign the contract for the public good to be built. If at least K of the N consumers sign the contract, then they each pay $S and the public good is built. If fewer than K do, then the public good is not created, and each who did sign gets $F.

How much value can a consumer expect to gain by signing or not signing the contract? Let X be a random variable equal to the number of other consumers who sign the contract, and let V be the consumer’s value of the public good. If the consumer doesn’t sign the contract, the public good is produced with probability P(X \geq K), producing expected value P(X \geq K) \cdot V for the consumer.

Alternatively, if the consumer does sign the contract, the probability that the public good is produced is P(X \geq K-1). In this condition, they get value V-S; otherwise, they get value F. Their expected value can then be written as P(X \geq K-1) \cdot (V - S) + (1 - P(X \geq K-1)) \cdot F.

The consumer will sign the contract if the second quantity is greater than the first, or equivalently, if the difference between the second and the first is positive. This difference can be written as:

P(X \geq K-1) \cdot (V - S) + (1 - P(X \geq K-1)) \cdot F - P(X \geq K) \cdot V

= P(X = K-1) \cdot V - P(X \geq K-1) \cdot S + (1 - P(X \geq K-1)) \cdot F

= P(X = K-1) \cdot V + F - P(X \geq K-1) \cdot (F + S).

Intuitively, the first term is the expected value the agents gains from signing by being pivotal, while the remaining terms express the agent’s expected value from success and failure payments.

This difference is monotonic in V. Therefore, each consumer has an optimal strategy consisting of picking a threshold value W and signing the contract when V > W (note: I write W instead of Tabarrok’s V*, for readability). This W value is, symmetrically, the same for each consumer, assuming that each consumer’s prior distribution over V is the same and these values are independent.

The distribution over X is, now, binomial with N-1 being the number of trials and P(V > W) being the probability of success. The probabilities in the difference can therefore be written as:

  • P(X = K-1) = \binom{N-1}{K-1} P(V > W)^{K-1} \left(1 - P(V > W)\right)^{N - K + 1}
  • P(X \geq K-1) = \sum_{x=K-1}^{N-1} \binom{N-1}{x} P(V > W)^x \left(1 - P(V > W)\right)^{N - x}.

By substituting these expressions into the utility difference P(X = K-1) \cdot V + F - P(X \geq K-1) \cdot (F + S), replacing V with W, and solving for this expression equaling 0 (which is true at the optimal W threshold), it is possible to solve for W. This allows expressing W as a function of F, S, and K. Specifically, when C = 0 and V is uniform in [0, 1], Tabarrok finds that, when the entrepreneur maximizes profit, P(V > W) ~= K/N. (I will not go into detail on this point, as it is already justified by Tabarrok)

The entrepreneur will set F, S, and K so as to maximize expected profit. Let Y be a binomially distributed random variable with N trials and a success probability of P(V > W), which represents how many consumers sign the contract. Let C be the cost the entrepreneur must pay to provide the public good. The entrepreneur’s expected profit is then

P(Y \geq K)(E[Y | Y \geq K]S - C) - P(Y < K)E[Y | Y < K]F

which (as shown in the paper) can simplified to

W K \binom{N}{K} P(V > W)^K P(V \leq W)^{N - K} - P(Y \geq K)C.

Note that probability terms involving Y depend on W which itself depends on F, S, K. Tabarrok analyzes the case where C = 0 and V is uniform in [0, 1], finding that the good is produced with probability approximately 0.5, K is approximately equal to N/2, W is approximately equal to N/2, and F is approximately equal to S.

To calculate profit, we plug these numbers into the profit equation, yielding:

N/4 \binom{N}{N/2} \cdot (1/2)^N.

Using the normal approximation of a binomial, we can estimate the term \binom{N}{N/2} (1/2)^N to be \mathrm{npdf}(N/2, N/4, N/2) = \mathrm{npdf}(0, N/4, 0) = 1/\sqrt{\pi N / 2}, where \mathrm{npdf}(\mu, \sigma^2, x) is the probability density of the distribution \mathcal{N}(\mu, \sigma^2) at x. Note that this term is the probability of every consumer being pivotal, P(Y = K); intuitively, the entrepreneur’s profit is coming from the incentive consumers have to contribute due to possibly being pivotal. The expected profit is then N/(4 \sqrt{\pi N / 2}) = \sqrt{N} / (4 \sqrt{\pi / 2}), which is proportional to \sqrt{N}.

The following is a plot of Y in the N=100 case; every consumer is pivotal at Y=50, which has approximately 0.08 probability.

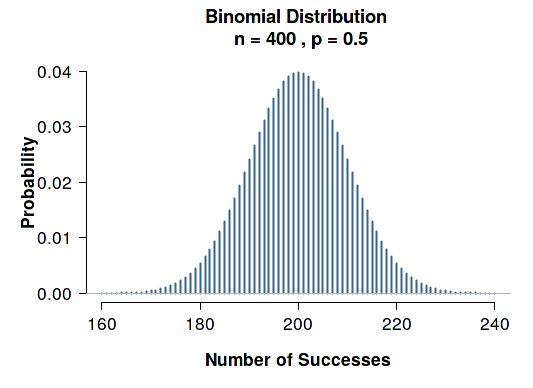
This second plot shows N=400; the probability of everyone being pivotal is 0.04, half of the probability in the N=100 case, showing a 1/\sqrt{N} scaling law for probability of being pivotal.

Tabarrok, however, claims that the expected profit in this case is proportional to N/2:

Setting V* to 1/2 and K to N/2 it is easy to check that expected profit is proportional to N/2 which is increasing in N.

This claim in the paper simply seems to be a mathematical error, although it’s possible I am missing something. In my 2012 essay, I derived that profit was proportional to \sqrt{N}, but didn’t point out that this differed from Tabarrok’s estimate, perhaps due to an intuition against openly disagreeing with authoritative papers.

We analyzed the case when V is uniform in [0, 1]; what if instead V is uniform in [0, Z]? This leads to simple scaling: W becomes Z/2 instead of 1/2, and expected profit is proportional to Z \sqrt{N}. This yields a scaling law for the profit that can be expected from a dominant assurance contract.

For some intuition on why profit is proportional to \sqrt{N}, consider that the main reason for someone to sign the contract (other than the success and failure payments, which don’t depend on V) is that they may be the pivotal person who produces the good. If you randomly answer N true-or-false questions, your mean score will be N/2, and the probability that a given question is pivotal (in terms of your score being above 50% just because of answering that question correctly) will be proportional to 1/\sqrt{N} by the normal approximation to a binomial. Introducing uncertainty into whether others sign the contract will, in general, put an upper bound on how pivotal any person can believe themselves to be, because they can expect some others to both sign and not sign the contract. Whereas, in the case where there was a positive lower bound on every consumer’s valuation, it was possible for a consumer to be 100% confident that the good would be produced if and only they signed the contract, implying a 100% chance of being pivotal.

The fact that profit in the uncertain valuation case scales with \sqrt{N} is a major problem for raising large amounts of money from many people with dominant assurance contracts. It is less of a problem when raising money from a smaller number of people, since \sqrt{N} is closer to N in those cases.

Excludable goods (such as copyrighted content) can in general raise revenue proportional to the total value created, even under uncertainty about consumer valuations. Dominant assurance contracts can function with non-excludable goods, however, this reduces the amount of expected revenue that can be raised.

[ED NOTE: since writing this post, I have found a corresponding impossibility result (example 8) in the literature, showing that revenue raised can only grow with \sqrt(n) where n is the number of consumers, under some assumptions.]

Published by Jessica Taylor

Leave a comment